What is a MIMO (Multi-Input Multi-Output) Model?

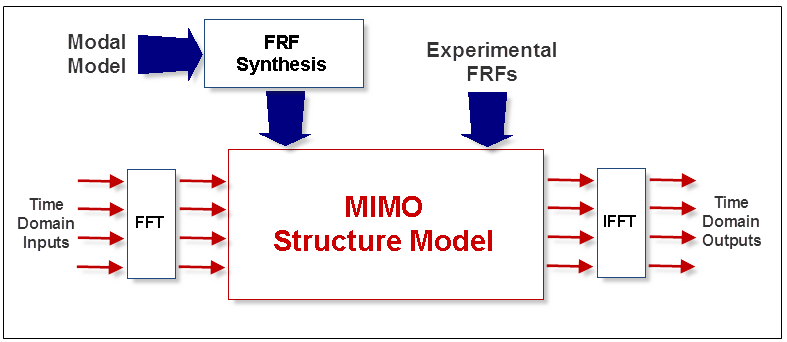
Calculation of multiple Inputs, Outputs & Transfer Functions of a structure is based upon the use of a MIMO (Multi-Input Multi-Output) dynamic model of the structure.  A MIMO model A MIMO model is a Multiple Input Multiple Output frequency domain matrix model containing a vector of Inputs, a matrix of Transfer functions and a vector of Outputs. The MIMO model is an equation where the Transfer function matrix is post-multiplied by the vector of Input DFTs to obtain the vector of Output DFTs. Inputs, Outputs & Transfer functions can be calculated using different forms of the MIMO model equation. is a frequency domain model where the Fourier spectra of multiple Inputs are multiplied by elements of a Transfer Function matrix to yield the Fourier spectra of multiple Outputs.  The MIMO model is written as,

{X(w)} = [H(w)] {F(w)}

where:

{F(w)} - Input Fourier spectra (m - vector)

[H(w)] - Transfer Function matrix (n by m)

{X(w)} - Output Fourier spectra (n - vector)

m - number of Inputs

n - number of Outputs

w - frequency variable (radians per second)

• Rows of the Transfer Function matrix correspond to Outputs and columns correspond to Inputs.

• Each Input and each Output corresponds to a DOF (point & direction) on a structure.

• Each Transfer Function is a cross-channel measurement between an Input DOF and an Output DOF.

MIMO Block Diagram

MIMO Calculations

Any part of a MIMO model, (Inputs, Outputs, or Transfer Functions) can be calculated from the other two parts.

• Inputs & Outputs can be either time or frequency domain measurement functions.

• Frequency domain measurements can be Fourier spectra, Auto & Cross spectra, and PSD's

• Transfer Functions can be either measured, or synthesized from a modal model A Modal Model is a set of mode shapes that have been scaled so that they preserve the dynamic properties of a structure. Two types of modal models are used in ME'scope, Residue mode shapes and Unit Modal Mass (UMM) mode shapes. Residue mode shapes are obtained by curve fitting a set of calibrated FRFs. UMM mode shapes are obtained by re-scaling a set of Residue mode shapes. Modal models are used for SDM calculations, FEA Model Updating, FRF synthesis, and MIMO calculations..

Transfer Function

A Transfer Function is defined as the Fourier spectrum of an Output divided by the Fourier spectrum of an Input.

Frequency Response Function (FRF)

An FRF is a special kind of Transfer Function.
An FRF is the Fourier spectrum of a displacement, velocity, or acceleration response divided by the Fourier spectrum of the excitation force that caused the response.

Transmissibility

A Transmissibility is a special kind of Transfer Function.
A Transmissibility is the Fourier spectrum of an Output divided by the Fourier spectrum of a Reference Output.