Residues and Mode Shapes

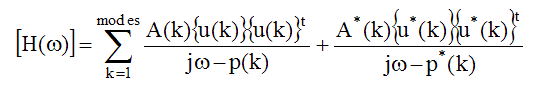
Key to Modal Testing: The relationship between residues and mode shapes is the key to modal testing.

The FRF matrix can be expressed in terms of modal poles & mode shapes as,

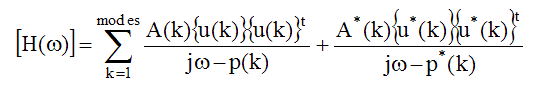
• p(k) = -s(k) + jw(k) = pole location of mode(k)  (Hz)

• A(k)  scaling constant for mode (k).

• {u(k)}  (n - vector).mode shape for the mode (k).

• t - denotes the transposed vector.

Relationship Between Residues and Mode Shapes

Each numerator is written in terms of a mode shape vector instead of a Residue A Residue is one of the three modal parameters (frequency & damping are the other two) obtained during FRF-based curve fitting. A Residue is the numerator term in the partial fraction expansion of the FRFcurve fitting model. A Residue is also referred to as the "strength" of the mode. Residue units are the FRF engineering units multiplied by Hz (or radians per second). Typical Residue units are g's/N-sec. matrix.  Comparing this equation with the previous partial fraction expansion of the MIMO model A MIMO model is a Multiple Input Multiple Output frequency domain matrix model containing a vector of Inputs, a matrix of Transfer functions and a vector of Outputs. The MIMO model is an equation where the Transfer function matrix is post-multiplied by the vector of Input DFTs to obtain the vector of Output DFTs. Inputs, Outputs & Transfer functions can be calculated using different forms of the MIMO model equation. yields the relationship between mode shapes and Residues .

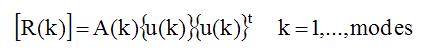
• Each mode shape (a column vector), is multiplied by itself transposed (a row vector).

• This vector product, (a column vector times a row vector), is called an outer product, and it yields a matrix.

• The resultant matrix multiplied by the scaling constant A(k) equals the Residue matrix.

A mode shape, (also called an eigenvector), is unique in shape but not in value.
A mode shape has no engineering units.
The scaling constant A(k) is required to make the right-hand side of the above equation equal to the Residue matrix, which contains unique values with engineering units

Mode Shape Scaling

Since scaling of mode shapes is arbitrary, the scaling constant A(k) can be chosen so that A(k) = 1.  This simplifies the equation between Residues and Mode Shapes ,

Fundamental Modal Testing Criterion

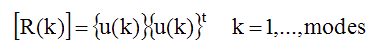
The following conclusions can be drawn from the above relationship between the residue matrix and mode shapes,

Every row and every column of the Residue matrix contains the mode shape multiplied by a different mode shape component
Any row or any column of the FRF matrix contains the same mode shape, for each mode (k)
Any row or any column of the FRF matrix can be measured and curve fit to extract the mode shape for each mode (k)

Mode Shape Node Points

The Residue equation indicates that if a row or column of the Residue matrix corresponds to a node point (zero value) of the mode shape, the entire row or column of residues is zero.

If a row or column of the Residue matrix corresponds to a node point of a mode shape, the numerators of all FRFs in the row & column are also zero
If a row or column of the Residue matrix corresponds to a node point of a mode shape, then none of the FRF measurements will contain a resonance peak as evidence of the mode.

When all modes of interest cannot be identified using a single row or column of the FRF matrix, multiple rows or columns are required. This requires multiple reference modal testing and multiple reference curve fitting.

Global Versus Local Modes

Many structures exhibit resonant vibration in a localized region of the structure.  Energy becomes "trapped" between stiff boundaries in a local region, and cannot readily escape, causing a standing wave of vibration, or local mode shape.

Global modes have mode shapes that are mostly non-zero, except at node points.
Local modes have mode shapes that are non-zero in a local region of the structure, and are zero elsewhere.