FRFs in Terms of Modal Parameters

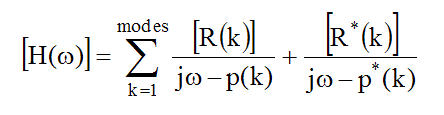
FRF An FRF (Frequency Response Function) is a cross-channel frequency domain function that defines the dynamic properties of a structure between an excitation Force and the Response caused by that force. An FRF is defined as the ratio (Response DFT / Force DFT). The FRF is a special case of a Transfer Function, where the response is the numerator (Output) and the force is the denominator (Input).-based curve fitting assumes that any FRF calculated between two DOFs of a vibrating structure can be completely represented in terms of modal parameters.

Partial Fraction Expansion of the FRF Matrix

The following parametric model is used to estimate experimental modal parameters by curve fitting FRF data.

• The FRF matrix is a summation of matrix pairs, each pair containing the contribution of a single mode (k).

• Each matrix pair for each mode (k) consists of a positive frequency term and a negative frequency (or complex conjugate) term.

• The unknown parameters of the parametric model are the modal frequency, damping & residue (mode shape component) for each mode of interest in the frequency band of the FRFs.

• The residues from a row or column of the FRF matrix are then saved as the mode shape for each mode.

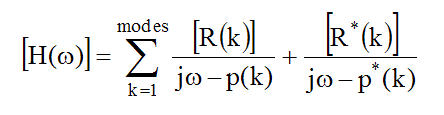
• [H(w)] - (n by n) FRF matrix.

• w -frequency variable     ( Hz or radians / second )

• p(k) - pole location for mode(k):  (p(k) = -s(k) + jw(k) )

• s(k) - damping decay constant for mode (k)   (in Hz or radians / second )

• w(k) - damped natural frequency for mode (k)     (in Hz or radians / second )

• [R(k)] - (n by n) Residue A Residue is one of the three modal parameters (frequency & damping are the other two) obtained during FRF-based curve fitting. A Residue is the numerator term in the partial fraction expansion of the FRFcurve fitting model. A Residue is also referred to as the "strength" of the mode. Residue units are the FRF engineering units multiplied by Hz (or radians per second). Typical Residue units are g's/N-sec. matrix for mode (k).

• n - number of DOFs of the MIMO model A MIMO model is a Multiple Input Multiple Output frequency domain matrix model containing a vector of Inputs, a matrix of Transfer functions and a vector of Outputs. The MIMO model is an equation where the Transfer function matrix is post-multiplied by the vector of Input DFTs to obtain the vector of Output DFTs. Inputs, Outputs & Transfer functions can be calculated using different forms of the MIMO model equation..

• modes - number of modes of interest on the structure.

• * - denotes the complex conjugate.

• j - denotes the imaginary axis in the complex plane.

Local versus Global Curve Fitting

Local curve fitting is necessary when physical changes such as mass loading, temperature changes, or other effects cause the resonant frequencies & damping to change during the course of a modal test.

• The denominators of each term in the FRF matrix contain the same modal frequency & damping.

• Since all of the denominators are the same, frequency & damping can be estimated by curve fitting a single FRF, or all FRFs taken from the test article.

Generally speaking, modes are global properties of a structure.  Therefore, each mode has only one frequency & damping value, and one mode shape.

• During Local curve fitting, each FRF is curve fit and local frequency & damping estimates are obtained for each mode and each FRF.

• During Global curve fitting, multiple FRFs are curve fit and only one global frequency & damping estimate is obtained for each mode.

Residue Matrix

A Residue represents the "strength" of a resonance.  That is, the stronger a resonance is relative to other resonances, the larger its residue will be.  In general, residues are complex numbers with magnitude & phase.

• In the partial fraction expansion equation, each mode (k) has a residue matrix [R(k)] associated with it.

• Each residue matrix has the same dimensions as the (n by n) MIMO model.

Residue units = ( FRF units ) x ( radians / second )
When one row or column of FRFs in the MIMO model is curve fit, the residues from the same row or column of the Residue matrix are estimated.

Parameter Estimation (Curve Fitting)

During curve fitting, four modal parameters are estimated for each mode (k),
Frequency & damping, or the pole location p(k) = -s(k) + jw(k).
Magnitude & phase of the complex Residue R(k).